Spring Stiffness Formula & Constant Calculation

Springs are fundamental components in many mechanical systems, and understanding their stiffness is crucial for effective design and application. In this article, we will talk about the concept of spring stiffness, its calculation methods, factors affecting it, and its applications in various industries.

1. What is Spring Stiffness?

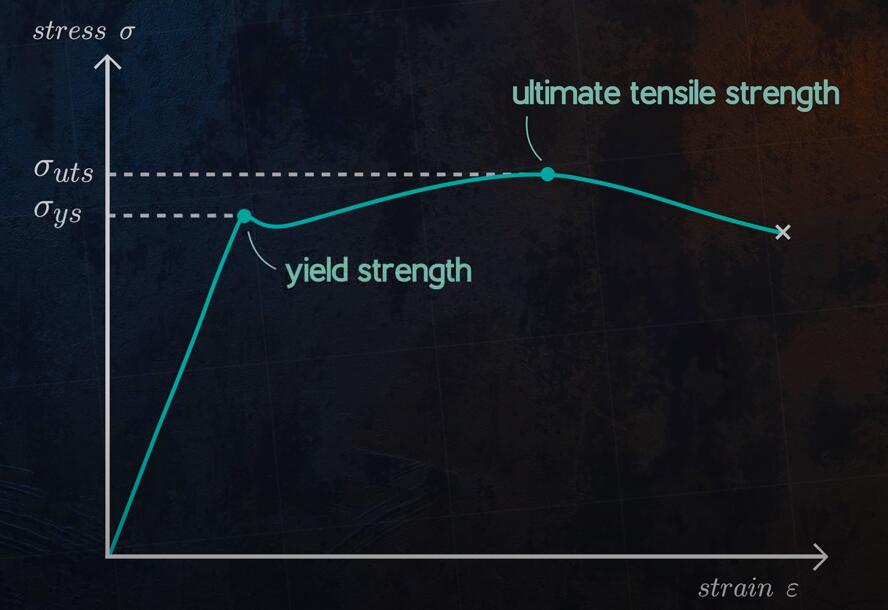
Spring stiffness refers to the property of a spring that describes how much it resists deformation when subjected to a force. It is defined as the ratio of the load increment (dF) to the deformation increment (dλ), meaning the load required to produce a unit deformation. The formula for spring stiffness is:

F’ = dF/dλ

Where:

• F′ is the stiffness of the spring,
• dF is the load increment,
• dλ is the deformation increment.

For linear springs, the stiffness remains constant regardless of the load, and this constant value is known as the spring constant. In this case, the stiffness can also be expressed as:

F′ = F/λ = constant

2. Types of Spring Stiffness

Springs can exhibit different stiffness characteristics based on their load-deformation relationship:

1. Increasing Stiffness: As the load increases, the spring stiffness increases.
2. Decreasing Stiffness: The stiffness decreases as the load increases.
3. Linear Stiffness: The stiffness remains constant regardless of the load, characteristic of linear springs.

For springs with linear behavior, the term spring constant is used interchangeably with stiffness. These springs are widely used due to their predictable and consistent performance.

3. Spring Stiffness Equation & Calculation for Different Spring Types

In spring testing, the stiffness of the spring can be calculated by measuring the applied force and deformation. The following is the calculation method for the stiffness of different springs:

a. Compression Spring Stiffness Formula

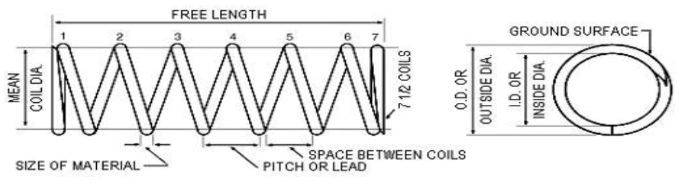
For compression springs, the maximum load and displacement size must also be calculated in addition to spring dimensions. Here is how to calculate the compression spring constant k (in kgf/mm) is:

k = G⋅d⁴ / 8⋅Dm³⋅Nc

Where:

• G: Modulus of rigidity for the wire material. For carbon steel wire G=79300, stainless steel wire G=697300, phosphor bronze wire G=4500, brass wire G=350.
• d: Wire diameter.
• Do​: Outer diameter (OD)
• Di: Inner diameter (ID)
• Dm​: Mean diameter Dm=Do−d
• N: Total number of coils.
• Nc: Effective number of coils, Nc=N−2

b. Tension Spring Stiffness Formula

The stiffness k of tension springs is calculated using the same formula as for compression springs.

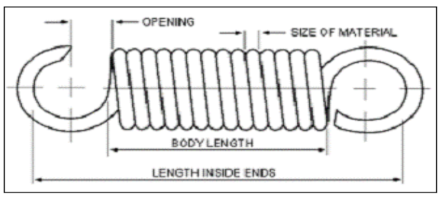
Initial tension: The initial tension is the force required to slightly separate the tightly bound coils of a tension spring. This tension occurs after the spring is wound into shape. Due to differences in material, wire diameter, spring index, static electricity, lubricants, heat treatment, and electroplating, each tension spring may have an inconsistent initial tension.
Here is how to calculate the tension spring constant k (in kgf/mm) is:

k = G⋅d⁴ / 8⋅Dm³⋅Nc

Where:

• G: Modulus of rigidity for the wire material. For carbon steel wire G=79300, stainless steel wire G=697300, phosphor bronze wire G=4500, brass wire G=350.
• d: Wire diameter.
• Do​: Outer diameter (OD)
• Di: Inner diameter (ID)
• Dm​: Mean diameter Dm=Do−d
• N: Total number of coils.
• Nc: Effective number of coils, Nc=N−2

c. Torsion Spring Stiffness Formula

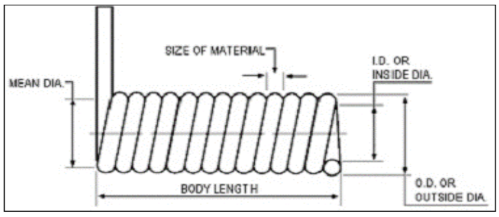
For torsion springs, the stiffness is related to the angle of twist. The torsion spring constant k (in kgf/mm per degree) is calculated using the formula:

k = E⋅d⁴ / 32⋅Dm⋅Nc⋅R

Where:

• E: Modulus of elasticity for the wire material. For piano wire E=21000, stainless steel wire E=19400, phosphor bronze wire E=11200, brass wire E=11200.
• d: Wire diameter.
• Do: Outer diameter (OD).
• Di: Inner diameter (ID).
• Dm: Mean diameter Dm=Do−d.
• N: Total number of coils.
• R: Load arm.
• p: Pi, p=3.1416.

4. Factors Affecting Spring Stiffness

Several factors influence the stiffness of a spring:

a. Material Properties

The stiffness of a spring is heavily dependent on the material from which it is made. Materials with a higher elastic modulus tend to produce springs with higher stiffness. Other material properties such as strength and hardness also play a role. For example, materials with higher strength typically result in stiffer springs.

b. Geometric Dimensions

The geometry of the spring, including its diameter, wire thickness, and length, is critical in determining its stiffness. Generally, smaller springs tend to have higher stiffness because they deform less under load compared to larger springs.

c. Manufacturing Process

Processes such as heat treatment and surface treatment can alter the mechanical properties of the spring material, thereby affecting its stiffness. Different treatments can either increase or decrease the stiffness depending on the desired spring characteristics.

d. Use Environment

Environmental factors, such as temperature, humidity, and the presence of corrosive gases, can impact the stiffness of a spring. For instance, increasing the temperature may cause the spring material to expand, reducing its stiffness, while lower temperatures may increase stiffness by contracting the material.

5. Testing Spring Stiffness

Testing the stiffness of a spring is essential for ensuring its performance and quality. Typically, a spring testing machine is used to apply a gradually increasing load to the spring while measuring the resulting deformation. The data is then processed to calculate the spring’s stiffness. There are several methods for testing spring stiffness:

• Static Testing: Measures stiffness under static load conditions.
• Dynamic Testing: Measures stiffness under dynamic or cyclic loading.
• Non-contact Testing: Uses advanced techniques such as laser measurement to determine stiffness without physically touching the spring.

6. Applications of Spring Stiffness

Spring stiffness plays a crucial role in various engineering applications. Some of the most common include:

• Aerospace: Springs are used in aircraft to absorb shocks and reduce vibrations during takeoff and landing.
• Automotive: Springs in vehicle suspensions and shock absorbers directly affect ride comfort, stability, and handling.
• Electronics and Instrumentation: Springs are used to provide precise movements and maintain tension in delicate instruments.

Understanding and calculating spring stiffness is vital in designing springs for specific applications. Whether it is a tension spring, compression spring, or torsion spring, the correct stiffness ensures that the spring performs its intended function effectively and reliably. By considering factors such as material properties, geometry, and environmental conditions, engineers can select and design springs with the appropriate stiffness for any given application.